常用的降维技术和主题模型简介

本文主要介绍了 LDA 主题模型及其在 R 语言中的实现方法

---

在机器学习中，LDA 是两个常用模型的简称：Linear Discriminant Analysis 和 Latent Dirichlet Allocation，这篇文章主要介绍后者。LDA (Latent Dirichlet Allocation) 是一种很常用的主题模型，类似于 LSA 和 PLSA 等模型，可以用于浅层语义分析，为了避免混淆，首先说明这些概念的区别。

---

Dimension Reduction Techniques

降维技术是很多主题模型的基础，常用的降维技术包括：PCA、FA、SVD 和 Linear Discriminant Analysis。其中 PCA、FA 和 SVD 主要关注未标记数据上的降维技术，但也可同时应用于已标记的数据，而 Linear Discriminant Analysis 则是针对已标记数据的降维技术

Principle Component Analysis

PCA（Principle Component Analysis）：主成分分析是一种降维技术，将过多的变量综合为少数几个概括性的新变量对原始目标进行解释。在主成分分析中，数据从原来的坐标系转换到了新的坐标系，新坐标系的选择由数据本身决定。第一个坐标轴选择原始数据中方差最大的方向，第二个坐标轴选择与第一个坐标轴正交且有最大方差的方向。重复此过程，大部分方差都会包含在前面的几个新坐标轴中，因此可以忽略余下的坐标轴，即对数据机进行了降维处理。

Factor Analysis

FA（Factor Analysis）：在因子分析中，假设在观察数据的生成过程中有一些观察不到的隐变量，假设观察数据是这些隐变量和某些噪声的线性组合，从而可以通过找到这些隐变量来实现数据的降维。

Singular Value Decomposition

SVD（Singular Value Decomposition）：奇异值分解是一种适用于任何矩阵的分解方法。假设原始矩阵 $A$ 是一个 $M \times N$ 的矩阵，那么可以将 $A$ 分解为：

$$A{m \times n}=U{m \times m} \Sigma{m \times n} V{n \times n}^T$$

• 上述分解会构造出一个矩阵 $\Sigma$，该矩阵为对角阵，除了对角元素，其他元素均为 0，惯例是 $\Sigma$ 中的元素从大到小排列，这些对角元素称为奇异值（Sigular Value）
• 和 PCA 中得到矩阵的特征值类似，奇异值也是告诉我们数据中的重要特征，奇异值与特征值的关系是：奇异值就是矩阵 $A \times A^T$ 特征值的平方根
• 如果矩阵 $\Sigma$ 的对角元素按从大到小排列，那么在某个数目（r 个）的奇异值之后，其他的奇异值都置为 0，这就意味着数据集中仅有 r 个重要特征，其余特征均是噪声或冗余特征

• 选取奇异值的数据，可以先计算奇异值的平方，然后将奇异值平方和累加到总值 90% 的数目作为最终选取的重要特征数

• 在推荐系统中的应用：简单的推荐系统能够计算 item 或 user 之间的相似度，从而进行基于内容的推荐或协同过滤推荐。进一步提升推荐效果的办法则是先利用 SVD 从数据（往往是一个非常稀疏的矩阵）中构建一个主题空间，然后再在该空间下计算其相似度。

Linear Discriminant Analysis

线性判别分析（Linear Discriminant Analysis），简称为 LDA，也被称为 Fisher 线性判别，是模式识别的经典算法。其基本思想是将高维的模式样本投影到最佳鉴别矢量空间，以达到抽取分类信息（分类）和压缩特征空间维数（降维）的效果，投影后保证模式样本在新的子空间有最大的类间距离和最小的类内距离，即模式在该空间中有最佳的可分离性。

LDA 与前面介绍过的 PCA 都是常用的降维技术。PCA 主要是从特征的协方差角度，去找到比较好的投影方式。LDA 更多的是考虑了标注，即希望投影后不同类别之间数据点的距离更大，同一类别的数据点更紧凑。

• PCA 降维是直接和数据维度相关的，比如原始数据是 n 维的，那么 PCA 后，可以任意选取 1 维、2 维，一直到 n 维都行（当然是对应特征值大的那些）。LDA 降维是直接和类别的个数相关的，与数据本身的维度没关系，比如原始数据是 n 维的，一共有 C 个类别，那么 LDA 降维之后，一般就是 1 维，2 维到 C-1 维进行选择（当然对应的特征值也是最大的一些）
• PCA 投影的坐标系都是正交的，而 LDA 根据类别的标注，关注分类能力，因此不保证投影到的坐标系是正交的（一般都不正交）

---

Basic Topic Models

在文本挖掘中，通常有很多文本文档，比如博客或新闻等，而我们的目的是将这些文本分成我们能够理解的不同类别。主题模型是一种无监督的文档分类方法，和对数值型数据进行聚类类似，主题模型是对文档进行“聚类”。

常用的主题模型包括 LSA（Latent Semantic Analysis）、PLSA（Probabilistic Latent Semantic Analysis） 和 LDA（Latent Dirichlet Allocation），但不管何种算法，主题模型的本质都是要计算两个矩阵

• Word 对 Topic 的矩阵
• Topic 对 Document 的矩阵

LSA

LSA 采用暴力 SVD 矩阵分解，如果维数太大，计算效率会很低。在 LSA 中，一个矩阵由文档和单词组成，当我们在矩阵上应用 SVD 时，就会构建出多个奇异值，每个奇异值代表文档中的一个概念或主题。

LSA 的具体实例参见 这篇博客

除了 LSA 之外，下面我们将介绍几个和 LDA 相关的基础模型：Unigram model、mixture of unigrams model、pLSA model。为了方便描述，首先定义一些变量：

• $w$ 表示词，$V$ 表示所有词的个数
• $z$ 表示主题，$k$ 表示主题的个数
• $D=(W_1,W_2,…,W_M)$表示语料库，M表示语料库中的文档数。
• $W=(w_1,w_2,…,w_N)$表示文档，N表示文档中词的个数。

Unigram Model

在一元模型中，对于文档 $W=(w_1,w_2,…,w_N)$ ，用 $p(w_n)$ 表示 $w_n$ 的先验概率，生成文档 $W$ 的概率为：

$$P(W)=\prod_{n=1}^n p(w_n)$$

其图模型为（图中被涂色的 w 表示可观测变量，N 表示一篇文档中总共 N 个单词，M 表示 M 篇文档）

Mixture of Unigrams Model

混合一元模型的生成过程是：给某个文档先选择一个主题 Z，再根据该主题生成文档，该文档中的所有词都来自一个主题。生成文档的概率

其图模型为（图中被涂色的 w 表示可观测变量，未被涂色的 z 表示未知的隐变量，N 表示一篇文档中总共 N 个单词，M 表示 M 篇文档）

PLSA

在混合一元模型中，假定一篇文档只由一个主题生成，可实际中，一篇文章往往有多个主题，只是这多个主题各自在文档中出现的概率大小不一样。在 PLSA 中，假设文档由多个主题生成。下面通过一个例子说明 PLSA 生成文档的过程

加入我们有三个主题，每个主题下有三个可选词，在生成文档的过程中，每写一个词，先扔“文档-主题”骰子选择主题，得到主题的结果后，使用和主题结果对应的那颗“主题-词项”骰子，扔该骰子选择要写的词。

• 上面这个投骰子产生词的过程简化一下便是：“先以一定的概率选取主题，再以一定的概率选取词”。事实上，一开始可供选择的主题有3个：教育、经济、交通，那为何偏偏选取教育这个主题呢？其实是随机选取的，只是这个随机遵循一定的概率分布。比如可能选取教育主题的概率是 0.5，选取经济主题的概率是 0.3，选取交通主题的概率是 0.2，那么这 3 个主题的概率分布便是{教育：0.5，经济：0.3，交通：0.2}，我们把各个主题 z 在文档 d 中出现的概率分布称之为主题分布，且是一个多项分布。
• 同样的，从主题分布中随机抽取出教育主题后，依然面对着3个词：大学、老师、课程，这3个词都可能被选中，但它们被选中的概率也是不一样的。比如大学这个词被选中的概率是0.5，老师这个词被选中的概率是0.3，课程被选中的概率是0.2，那么这3个词的概率分布便是{大学：0.5，老师：0.3，课程：0.2}，我们把各个词语 w 在主题 z 下出现的概率分布称之为词分布，这个词分布也是一个多项分布。
• 最后，不停的重复扔“文档-主题”骰子和”主题-词项“骰子，重复 N 次（产生 N 个词），完成一篇文档，重复这产生一篇文档的方法 M 次，则完成 M 篇文档

利用看到的文档推断其隐藏的主题（分布）的过程，就是主题建模的目的：自动地发现文档集中的主题（分布）。文档 d 和单词 w 是可被观察到的，但主题 z 却是隐藏的。如下图所示（图中被涂色的 d、w 表示可观测变量，未被涂色的 z 表示未知的隐变量，N 表示一篇文档中总共 N 个单词，M 表示 M 篇文档）。

对于任意一篇文档，$P(w_j|d_i)$ 是已知的，根据这个概率可以训练得到“文档-主题”概率以及“主题-词项”概率，即：

每篇文档中每个词的生成概率为：

$P(d_i)$ 可以直接得出，而 $P(z_k|d_i)$ 和 $P(w_j|z_k)$ 未知，所以 $\theta=(P(z_k|d_i),P(w_j|z_k))$就是我们要估计的参数，我们要最大化这个参数。因为该待估计的参数中含有隐变量 z，所以我们可以用 EM 算法来估计这个参数。

PLSA 把 LSA 变成从概率的角度理解，把 LSA 的 2 个矩阵做归一化处理后，就可以看成 PLSA 的 Word 对于 Topic 的概率分布和 Document 对于 Topic 的概率分布。然后采用 EM 算法，先随机初始化这 2 个分布，计算其后验概率，然后反过来利用最大似然来计算这 2 个分布，不断迭代直到收敛，但 PLSA 已经基本上被 LDA 所取代。

---

LDA Topic Model

LDA（Latent Dirichlet Allocation, 潜狄利克雷分布）是一种概率主题模型，它在 PLSA 的基础上，利用贝叶斯估计，引入 Topic 的 Dirichlet 先验分布后得到贝叶斯模型，相当于多了一个条件，而后采用 Gibbs sampling 的方式来学习参数，收敛后计算得到 Word 对于 Topic 的概率分布和 Topic 对于 Document 的概率分布。

在 PLSA 中，样本随机，参数虽未知但固定，所以 PLSA 属于频率派思想。区别于下文要介绍的LDA中，样本固定，参数未知但不固定，是个随机变量，服从一定的分布，所以 LDA 属于贝叶斯派思想。

LDA 涉及的数学知识很多，包括 Gamma 函数、Dirichlet 分布、Dirichlet-Multinomial 共轭、Gibbs Sampling、Variational Inference、PLSA 等，暂且不论其背后的数学逻辑，理解 LDA 模型最重要的两点是

• 每个文档由多个主题构成，例如 “Document 1 由 90% 的 Topic A 和 10% 的 Topic B 构成”
• 每个主题由多个单词构成，例如 “政治主题最常见的单词是 President、Congress 和 Government”

LDA是一种典型的词袋模型，即它认为一篇文档是由一组词构成的一个集合，词与词之间没有顺序以及先后的关系。一篇文档可以包含多个主题，文档中每一个词都由其中的一个主题生成。

Mathematical Basis

Beta-Binomial Conjugate

• Beta 分布可以看做是概率的概率分布，当你不确定一个事件的具体概率是多少时，它可以给出了所有概率出现的可能性大小。Beta 分布的概率密度函数如下，B 函数是一个标准化函数，它只是为了使得这个分布的概率密度积分等于 1 才加上的。

  , where

• 二项分布是由伯努利分布推出的。伯努利分布，又称两点分布或 0-1 分布，是一个离散型的随机分布，其中的随机变量只有两类取值，即 0 或 1。二项分布是重复 n 次的伯努利试验。简言之，只做一次实验，是伯努利分布，重复做了 n 次，是二项分布。二项分布的概率密度函数为

$$P(K=k)=C(n,k)p^k(1-p)^{n-k}, where \ C(n,k)=\frac{n!}{k!(n-k)!}$$

• 轭的意思是束缚、控制。共轭（conjugate）从字面上理解，则是共同约束，或互相约束。在贝叶斯概率理论中，如果后验概率 $P(z|x)$ 和先验概率 $p(z)$ 满足同样的分布，那么，先验分布和后验分布被称为共轭分布，同时，先验分布叫做似然函数的共轭先验分布。

  • 二项分布的似然函数为 $P(data|\theta)\propto \theta^k (1-\theta)^{n-k}$
  • Beta 分布为：$Beta(\alpha,\beta)=\theta^{\alpha-1}(1-\theta)^{\beta-1}/B(\alpha,\beta) \propto \theta^{\alpha-1}(1-\theta)^{\beta-1}$
  • 贝叶斯估计的目的就是要在给定数据的情况下求出参数 θ 的值，所以我们的目的是求解后验概率，因为 data 与待估参数独立，所以不予考虑，我们称 $P(data|\theta)$ 为似然函数，$P(\theta)$ 为先验分布

  $$P(\theta|data)=\frac{P(data|\theta)P(\theta)}{P(data)}\propto P(data|\theta)P(\theta)$$

  • 现在我们将服从 Beta 分布的先验分布带入可以得到
    $$P(\theta|data)=\theta^k (1-\theta)^{n-k}\ * \ \theta^{\alpha-1}(1-\theta)^{\beta-1}\ \propto \theta^{\alpha+k-1}(1-\theta)^{\beta+n-k-1}$$
  • 因此，贝叶斯估计得到的后验概率仍然服从 Beta 分布，所以说 Beta 分布是二项分布的共轭先验分布！

下面举一个简单的例子来说明 Beta 分布和二项分布是共轭分布，熟悉棒球运动的都知道有一个指标就是棒球击球率 (batting average)，就是用一个运动员击中的球数除以击球的总数，我们一般认为 0.266 是正常水平的击球率，而如果击球率高达 0.3 就被认为是非常优秀的。现在有一个棒球运动员，我们希望能够预测他在这一赛季中的棒球击球率是多少。你可能就会直接计算棒球击球率，用击中的数除以击球数，但是如果这个棒球运动员只打了一次，而且还命中了，那么他就击球率就是 100% 了，这显然是不合理的，因为根据棒球的历史信息，我们知道这个击球率应该是 0.215 到 0.36 之间才算正常。

对于这个问题，我们可以用一个二项分布表示（一系列成功或失败），表示这些经验最好的方法（在统计中称为先验信息）就是用 beta 分布，这表示在我们没有看到这个运动员打球之前，我们就有了一个大概的范围。beta 分布的定义域是(0,1)，这跟概率的范围是一样的。

接下来我们将这些先验信息转换为 beta 分布的参数，我们知道一个击球率应该是平均 0.27 左右，而他的范围是 0.21 到 0.35，那么根据这个信息，我们可以取 $\alpha=81、\beta=219$。那么，$Beta(\alpha,\beta)$ 分布的均值为：$mean=\frac{\alpha}{\alpha+\beta}=\frac{81}{81+219}=0.27$。

如下图中的红线所示，x 轴就表示各个击球率的取值，x 对应的 y 值就是这个击球率所对应的概率。也就是说 beta 分布可以看作一个概率的概率分布。那么有了先验信息后，现在我们考虑一个运动员只打一次球，那么他现在的数据就是“1击1中”，即 hit=1/miss=0。这时候我们就可以更新我们的分布了，让这个曲线做一些移动去适应我们的新信息。beta 分布在数学上就给我们提供了这一性质，他与二项分布是共轭先验的（Conjugate_prior）。所谓共轭先验就是先验分布是 $Beta(\alpha,\beta)$ 分布，而后验分布同样是 beta 分布： $Beta(\alpha+hit,\beta+miss)=Beta(81+1,219+0)$。

如下图中的绿线所示，可以看出更新之后的 PDF 变化不大，因为只打一次球并不能说明什么问题。但如果我们有更多的数据，比如一共打了 300 次，击中 100 次，未击中 200 次，再次更新之后 PDF 变为： $Beta(81+100,219+200)$。

如下图中的蓝线所示，可以看到更新后的曲线变得更尖，并且向右平移了一段距离，说明比平均水平要高。新分布的数学期望为 $\frac{181}{181+419}=0.302$，这比直接估计的结果 $\frac{100}{100+200}=0.333$ 小，这是因为我们包含了先验信息，可以理解为在这个运动员在击球之前他已经成功了 81 次，失败了 219 次。

Dirichlet-Multinomial Conjugate

• Dirichlet 分布式 Beta 分布在高维度上的推广，两者的 PDF 类似：

  where

• 多项分布（Multinomial Distribution）是二项分布在高纬度上的推广，多项分布是指单次试验中的随机变量的取值不再是0-1，而是有多种离散值可能（1,2,3…,k）。比如投掷 6 个面的骰子，N 次实验结果服从 K=6 的多项分布。

• Dirichlet 和 Multinomial 共轭分布的证明较为复杂，暂不深究，但道理和 Beta-Binomial 共轭类似。至此，我们可以看到二项分布和多项分布很相似，Beta 分布和 Dirichlet 分布很相似。并且 Beta 分布是二项式分布的共轭先验概率分布。同样道理，Dirichlet 分布是多项式分布的共轭先验概率分布。

Document Generation Process

当我们看到一篇文章后，往往会推测这篇文章是如何生成的，我们通常认为作者会先确定几个主题，然后围绕这几个主题遣词造句写成全文。LDA 要干的事情就是根据给定的文档，判断它的主题分布，以及每个主题下的单词分布。如下图所示，在 LDA 模型中，生成文档的过程有以下几步：

1. 从狄利克雷分布 $\alpha$ 中生成文档 $i$ 的主题分布 $\theta_i$
2. 从主题的多项式分布 $\thetai$ 中取样生成文档 $i$ 第 $j$ 个词的主题 $Z{i,j}$
3. 从狄利克雷分布 $\beta$ 中取样生成主题 $Z{i,j}$ 对应的词语分布 $\Phi{i,j}$
4. 从词语的多项式分布 $\Phi{i,j}$ 中采样最终生成词语 $W{i,j}$

在 LDA 网络的贝叶斯结构中，阴影圆圈表示可观测的变量，非阴影圆圈表示隐变量，箭头表示两变量间的条件依赖性 （conditional dependency），方框表示重复抽样，方框右下角的数字代表重复抽样的次数。$\varphi$ (Topic-Word 分布) 和 $\theta$ (Doc-Topic 分布) 是 Dirichlet distributions， $\theta$ 指向 $Z$ 是从 Doc-Topic 分布中采样一个主题赋给 $W$，$\varphi$ 指向 $W$ 是 $\varphi$ 的 Topic-Word 分布依赖于 $W$。

• $K$ 表示主题数，$N$ 表示各文档中的单词数，$M$ 表示文档数
• $\alpha$ 是 Document-Topic 的 Dirichlet-prior Distribution
• $\beta$ 是 Topic-Word 的 Dirichlet-prior Distribution
• $\theta_i$ 是文档 $i$ 的主题分布
• $\varphi_k$ 是主题 $k$ 的单词分布
• $W_{i,j}$ 是文档 $i$ 的单词 $j$
• $Z{i,j}$ 是 $W{i,j}$ 对应的主题

拿之前讲解 PLSA 的例子进行具体说明。如前所述，在 PLSA中，选主题和选词都是两个随机的过程，先从主题分布{教育：0.5，经济：0.3，交通：0.2}中抽取出主题：教育，然后从该主题对应的词分布{大学：0.5，老师：0.3，课程：0.2}中抽取出词：大学。举个文档d产生主题z的例子。在 PLSA 中，给定一篇文档 d，主题分布是一定的，比如 {P(zi|d), i = 1,2,3}可能就是 {0.4,0.5,0.1}，表示 z1、z2、z3 这3个主题被文档 d 选中的概率都是个固定的值：P(z1|d) = 0.4、P(z2|d) = 0.5、P(z3|d) = 0.1，如下图所示:

而在LDA中，选主题和选词依然都是两个随机的过程，但是主题分布和词的分布不再唯一确定不变，即无法确切给出。例如主题分布可能是{教育：0.5，经济：0.3，交通：0.2}，也可能是{教育：0.6，经济：0.2，交通：0.2}，到底是哪个我们不能确定，因为它是随机的可变化的。但再怎么变化，也依然服从一定的分布，主题分布和词分布由 Dirichlet 先验确定。

换言之，LDA 在 PLSA 的基础上给 $P(z_k|d_i)$ 和 $P(w_j|z_k)$ 这两个参数加了两个先验分布（贝叶斯化）。

综上，LDA 真的只是 PLSA 的贝叶斯版本，文档生成后，两者都要根据文档去推断其主题分布和词语分布（即两者本质都是为了估计给定文档生成主题，给定主题生成词语的概率），只是用的参数推断方法不同，在 PLSA 中用极大似然估计的思想去推断两未知的固定参数，而 LDA 则把这两参数弄成随机变量，且加入 dirichlet 先验。所以，PLSA跟 LDA 的本质区别就在于它们去估计未知参数所采用的思想不同，前者用的是频率派思想，后者用的是贝叶斯派思想。

比如，我去一朋友家：

• 按照频率派的思想，我估计他在家的概率是 1/2，不在家的概率也是 1/2，是个定值
• 而按照贝叶斯派的思想，他在家不在家的概率不再认为是个定值 1/2，而是随机变量。比如按照我们的经验（比如当天周末），猜测他在家的概率是 0.6，但这个 0.6 不是说就是完全确定的，也有可能是 0.7。如此，贝叶斯派没法确切给出参数的确定值，但至少明白在哪个范围或哪些取值（0.6、0.7、0.8、0.9）更有可能，哪个范围或哪些取值（0.3、0.4） 不太可能。进一步，贝叶斯估计中，参数的多个估计值服从一定的先验分布，而后根据实践获得的数据（例如周末不断跑他家），不断修正之前的参数估计，从先验分布慢慢过渡到后验分布

LDA 生成文档的过程中，先从 dirichlet 先验中“随机”抽取出主题分布，然后从主题分布中“随机”抽取出主题，选取不同的参数 $\alpha$，dirichlet 分布会偏向不同的主题。Document-Topic 和 Topic-Word 的 Dirichlet-Multinomial 共轭结构如下图：

Parameter Estimation

• 在 PLSA 中，我们使用 EM 算法去估计“主题-词项”矩阵和“文档-主题”矩阵这两个参数，而且这两参数都是个固定的值，只是未知，使用的思想其实就是极大似然估计 MLE。
• 而在 LDA 中，估计这两未知参数可以用变分 (Variational inference)-EM算法，也可以用 gibbs 采样，前者的思想是最大后验估计MAP（MAP与MLE类似，都把未知参数当作固定的值），后者的思想是贝叶斯估计。贝叶斯估计是对 MAP 的扩展，但它与 MAP 有着本质的不同，即贝叶斯估计把待估计的参数看作是服从某种先验分布的随机变量.

LDA 的原始论文中是用的“变分-EM”算法估计未知参数，后来发现另一种估计 LDA 未知参数的方法更好，这种方法就是：Gibbs Sampling。Gibbs 采样是马尔可夫链蒙特卡尔理论（MCMC）中用来获取一系列近似等于指定多维概率分布（比如 2 个或者多个随机变量的联合概率分布）观察样本的算法，Gibbs Sampling 的大致流程如下：

基于上述 LDA 模型的文档生成过程，整个模型所有可见变量以及隐藏变量的联合分布是

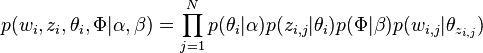
最终一篇文档的单词分布的最大似然估计可以通过将上式的 $\theta_i$ 以及 $\Phi$ 进行积分和对 $z_i$ 进行求和得到。然后，根据 $p(w_i|\alpha ,\beta )$ 的最大似然估计，最终可以通过吉布斯采样等方法估计出模型中的参数。

因为 $\alpha$ 产生主题分布 $\theta$，主题分布 $\theta$ 确定具体主题，且 $\beta$ 产生词分布 $\varphi$、词分布 $\varphi$ 确定具体词，所以所有变量的联合概率分布其实等价于：

$$p(w,z|\alpha,\beta)=p(z|\alpha)p(w|z,\beta)$$

由于此公式第一部分独立于 $\beta$，第二部分独立于 $\alpha$，所以可分别处理。根据贝叶斯法则和 Dirichlet 先验，以及上文中得到的 $p(z|\alpha)$ 和 $p(w|z,\beta)$ 各自被分解成两部分乘积的结果可以计算得到每个文档上 Topic 的后验分布和每个 Topic 下的词的后验分布（据上文可知：其后验分布跟它们的先验分布一样，也都是 Dirichlet 分布），最终求解 Topic-Word 和 Doc-Topic 的 Dirichlet 分布的期望为：

具体的推导过程参见 这篇博客

这样就计算出了最终我们要求的分布参数（注意分布参数的计算要在 sampling 收敛阶段进行）。有了 Dirichlet 后验分布的期望，排除当前词的主题分配，即根据其他词的主题分配和观察到的单词来计算当前词主题的概率公式为

这个式子的右半部分便是 $p(Topic|Doc)*p(Word|Topic)$，这个概率的值对应 $Doc\rightarrow Topic \rightarrow Word$ 的路径概率。如此，K 个 Topic 对应着 K 条路径，Gibbs Sampling 便在这 K 条路径中进行采样，如下图所示:

Gibbs Sampling in LDA

第一阶段：初始化

• 输入单词向量 $w$，超参数 $\alpha$ 和 $\beta$，主题数 $K$
• 全局变量：$n_m^{(k)}$ 文档 m 中 主题 k 出现的次数；$n_m$ 文档 m 中的主题总数；$n_k^{(t)}$ 主题 k 中单词 t 出现的次数；$n_k$ 主题 k 中的单词总数。将这四个全局变量全部初始化为 0。
• 对所有文档 $m\in [1,M]$：
  • 对文档 $m$ 中的所有单词 $n$：
    • 采样每个单词对应的主题 $z_{m,n}=k~Mult(1/K)$
    • 增加“文档-主题”计数：$n_m^{(k)}+=1$
    • 增加“文档-主题”总数：$n_m+=1$
    • 增加“主题-词项”计数：$n_k^{(t)}+=1$
    • 增加“主题-词项”总数：$n_k+=1$

第二阶段：burn-in（Gibbs 未收敛阶段）

• 对所有文档 $m\in [1,M]$：
  • 对文档 $m$ 中的所有单词 $n$：
    • 假如当前文档 $m$ 的词 $t$ 对应主题为 $k$，减少计数 $n_m^{(k)}-=1$，$n_m-=1$，$n_k^{(t)}-=1$，$n_k-=1$，即先拿出当前词
    • 之后根据 LDA 中 Topic sample 的概率分布 sample 出新的主题，然后对应的四个全局变量再分别 +1

第三阶段：sampling（Gibbs 收敛阶段）

• 迭代完成后，输出 Topic-Word 参数矩阵 $\phi$ 和 Doc-Topic 矩阵 $\theta$

---

Latent Dirichlet Allocation in R

Document-Term Matrix

文本挖掘最常见的数据结构 Document-Term Matrix (or DTM)，通常情况下：

• 行代表 Document（比如一本书或一篇文章）
• 列代表 Term
• 矩阵的值代表 Term 在 Document 中出现的次数

但一般来说，DTM 都是一个十分稀疏的矩阵，因此在 R 中会有专门的数据结构对其进行更有效率的存储。

DocumentTermMatrix (tm)

R 中最常用的 DTM 数据结构是 tm 包中的 DocumentTermMatrix，很多文本挖掘的数据集都以这种形式提供，例如美联社新闻数据集，包括 2246 篇文档和 10473 个单词，稀疏度 99% 表示 DTM 中 99% 的值为 0。

library(Topicmodels)
data("AssociatedPress")
AssociatedPress

## <<DocumentTermMatrix (Documents: 2246, terms: 10473)>>
## Non-/sparse entries: 302031/23220327
## Sparsity           : 99%
## Maximal term length: 18
## Weighting          : term frequency (tf)

tbl_df (dplyr)

如果我们想用 dplyr、tidytext、ggplot2 等包对文档进行分析，则需要将 DTM 转换为 one-token-per-Document-per-row 的形式，该形式只保留非零值。

library(dplyr)
library(tidytext)
ap_td <- tidy(AssociatedPress)
ap_td

## # A tibble: 302,031 × 3
##    Document       term count
##       <int>      <chr> <dbl>
## 1         1     adding     1
## 2         1      adult     2
## 3         1        ago     1
## 4         1    alcohol     1
## 5         1  allegedly     1
## 6         1      allen     1
## 7         1 apparently     2
## 8         1   appeared     1
## 9         1   arrested     1
## 10        1    assault     1
## # ... with 302,021 more rows

然后，我们就可以对其进行包括情感分析在内的诸多分析。

ap_sentiments <- ap_td %>%
  inner_join(get_sentiments("bing"), by = c(term = "Word"))

ap_sentiments
## # A tibble: 30,094 × 4
##    Document    term count sentiment
##       <int>   <chr> <dbl>     <chr>
## 1         1 assault     1  negative
## 2         1 complex     1  negative
## 3         1   death     1  negative
## 4         1    died     1  negative
## 5         1    good     2  positive
## 6         1 illness     1  negative
## 7         1  killed     2  negative
## 8         1    like     2  positive
## 9         1   liked     1  positive
## 10        1 miracle     1  positive
## # ... with 30,084 more rows

# 最长用的正面词和负面词
library(ggplot2)
ap_sentiments %>%
  count(sentiment, term, wt = count) %>%
  ungroup() %>%
  filter(n >= 200) %>%
  mutate(n = ifelse(sentiment == "negative", -n, n)) %>%
  mutate(term = reorder(term, n)) %>%
  ggplot(aes(term, n, fill = sentiment)) +
  geom_bar(stat = "identity") +
  ylab("Contribution to sentiment") +
  coord_flip()

LDA Code in R

用 R 中 Topicmodels 包中的 LDA 函数实现主题模型，以主题数 k=2 为例

# set a seed so that the output of the model is predictable
ap_lda <- LDA(AssociatedPress, k = 2, control = list(seed = 1234))
ap_lda
## A LDA_VEM Topic model with 2 Topics.

然后，用 tidytext 包中的 tidy() 方法可以从 LDA() 的结果中提取 Word-Topic probabilities 和 Document-Topic probabilities

Word-Topic Probabilities

library(tidytext)
ap_Topics <- tidy(ap_lda, matrix = "beta")
ap_Topics

## # A tibble: 20,946 × 3
##    Topic       term         beta
##    <int>      <chr>        <dbl>
## 1      1      aaron 1.686917e-12
## 2      2      aaron 3.895941e-05
## 3      1    abandon 2.654910e-05
## 4      2    abandon 3.990786e-05
## 5      1  abandoned 1.390663e-04
## 6      2  abandoned 5.876946e-05
## 7      1 abandoning 2.454843e-33
## 8      2 abandoning 2.337565e-05
## 9      1     abbott 2.130484e-06
## 10     2     abbott 2.968045e-05
## # ... with 20,936 more rows

从中，我们可以看出每个 Word 由各个 Topic 产生的概率，比如 “arron” 有 1.686917e-12 的概率由 Topic 1 产生，有 3.895941e-05 的概率由 Topic 2 产生。除此之外，可以进一步统计每个 Topic 中出现最多的词，以及在两个 Topic 中差异最大的词

Document-Topic probabilities

ap_Documents <- tidy(ap_lda, matrix = "gamma")
ap_Documents

## # A tibble: 4,492 × 3
##    Document Topic        gamma
##       <int> <int>        <dbl>
## 1         1     1 0.2480616686
## 2         2     1 0.3615485445
## 3         3     1 0.5265844180
## 4         4     1 0.3566530023
## 5         5     1 0.1812766762
## 6         6     1 0.0005883388
## 7         7     1 0.7734215655
## 8         8     1 0.0044516994
## 9         9     1 0.9669915139
## 10       10     1 0.1468904793
## # ... with 4,482 more rows

从 Document-Topic 概率中，我们可以看出每个文档的词由各个主题产生的比例。比如，Document 1 中只有 24.8% 的词是由 Topic 1 产生的，而 Document 6 中几乎所有的词都由 Topic 2 产生（可以通过查看 Document 6 中的词验证其确实属于政治主题）。

tidy(AssociatedPress) %>%
  filter(Document == 6) %>%
  arrange(desc(count))

## # A tibble: 287 × 3
##    Document           term count
##       <int>          <chr> <dbl>
## 1         6        noriega    16
## 2         6         panama    12
## 3         6        jackson     6
## 4         6         powell     6
## 5         6 administration     5
## 6         6       economic     5
## 7         6        general     5
## 8         6              i     5
## 9         6     panamanian     5
## 10        6       american     4
## # ... with 277 more rows

更多文本挖掘和 LDA 可视化的详细介绍参见 Reference：Topic Modeling in R

---

Reference

• Latent Dirichlet Allocation
  • Blei, D. M., Ng, A. Y., & Jordan, M. I. (2003). Latent dirichlet allocation. Journal of machine Learning research, 3(Jan), 993-1022.
  • Latent Dirichlet Allocation from Github.com
  • 主题模型TopicModel：隐含狄利克雷分布LDA - CSDN.NET. (2017). Blog.csdn.net. Retrieved 21 April 2017
  • 隐含狄利克雷分布 | Wikiwand. (2017). Wikiwand. Retrieved 21 April 2017
  • 通俗理解LDA主题模型 - CSDN.NET. (2017). Blog.csdn.net. Retrieved 21 April 2017
  • LDA 数学八卦, Rickjin, Version 1
• Distribution
  • Beta distribution | Wikiwand. (2017). Wikiwand. Retrieved 21 April 2017
  • (2017). 如何通俗地理解 Beta 分布. Zhihu.com. Retrieved 21 April 2017
  • Dirichlet distribution | Wikiwand. (2017). Wikiwand. Retrieved 21 April 2017
  • Multinomial distribution | Wikiwand. (2017). Wikiwand. Retrieved 21 April 2017
• Topic Modeling in R
  • Robinson, J. (2017). Text Mining with R. Tidytextmining.com. Retrieved 14 April 2017
  • David Meza. (2017). Topic Modeling in R. Retrieved 19 April 2017
• Others
  • 《机器学习实战》 哈林顿 (Peter Harrington), 李锐, 李鹏, 曲亚东, 王斌. (2017). Amazon.cn. Retrieved 14 April 2017
  • LDA 线性判别分析 - porly的专栏 - 博客频道 - CSDN.NET. (2017). Blog.csdn.net. Retrieved 14 April 2017
  • (2017). LDA 与 LSA、PLSA、NMF相比，哪个效果更好？为什么？Zhihu.com. Retrieved 14 April 2017
  • 机器学习中的数学(5)-强大的矩阵奇异值分解(SVD)及其应用 - LeftNotEasy - 博客园. (2017). Cnblogs.com. Retrieved 14 April 2017
  • Latent Semantic Analysis (LSA) Tutorial. (2011). Personal Wiki. Retrieved 14 April 2017